Neulich hatten wir uns in die Lage eines Managers versetzt, der für des Ergebnis eines Webshops verantwortlich ist. Er bekommt regelmäßig Auswertungen mit den Bestellzahlen vom Vortag. Nachdem wir gemerkt hatten, dass diese Werte für sich allein genommen nicht wirklich interpretierbar sind, hatten wir uns Diagramm für die tägliche Anzahl Bestellungen der letzten Wochen angesehen:

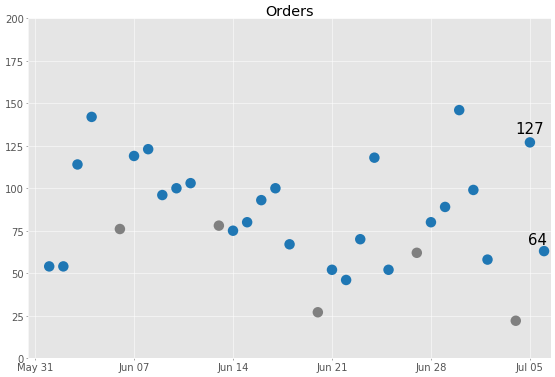
Nach 127 Bestellungen vom 5. Juli waren es nur noch 64 Bestellungen am 6. Juli. Obwohl sich die Anzahl Bestellungen im Vergleich zum Vortag halbiert hatte, sieht es gar nicht mehr so beunruhigend aus, wenn man berücksichtigt, wie groß die Schwankungen in der Vergangenheit waren.

Ab wo sollten wir Alarm schlagen wegen zu weniger Bestellungen? Ab wo sollten wir aufmerken, weil es wesentlich mehr Bestellungen als sonst gab? Und wann wird aus zufälligen Schwankungen einen Trend nach oben oder unten?

Vergleichszeitraum auswerten

Um diese Fragen beantworten zu können, muss man die “normalen Schwankungen” in der Bestellzahl irgendwie fassen. Dazu legt man einen Vergleichszeitraum fest, hier könnte es das erste Quartal sein:

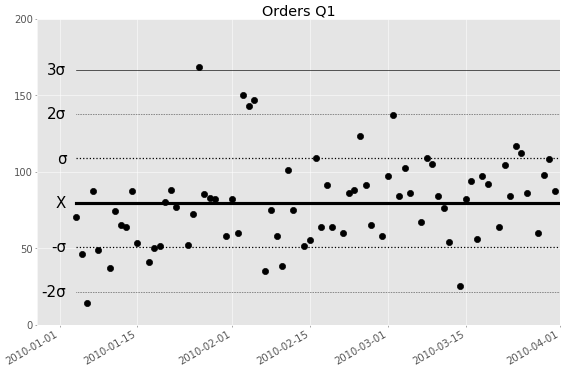
Der Vergleichszeitraum sollte möglichst frei von Saison- und Sondereffekten sein.

Die mittlere Anzahl Bestellungen liegt im ersten Quartal bei 80 (genauer: 79,6), das habe ich als fette schwarze Linie (beschriftet mit X) eingezeichnet. Die Punkte streuen um diesen Mittelwert, mal sind es mehr, mal weniger als 80 Bestellungen. Die Schwankungsbreite wird durch den statistischen Parameter Standardabweichung (a.k.a. Streuung) angegeben, bezeichnet mit dem griechischen Buchstaben Sigma, σ. (Von diesem Sigma hat übrigens das Six-Sigma Managementsystem seinen Namen.) In unserem Diagramm beträgt die Streuung 29,0. Die dünnen Linien verlaufen bei einer, zwei bzw. drei Standardabweichungen ober- und unterhalb des Mittelwertes. Für die nötigen Berechnungen von Mittelwert und Standardabweichung gibt es Formeln in Excel.

Aufgrund der Erfahrungen aus dem ersten Quartal sagen wir nun:

“Unser Webshop bekommt an normalen Tagen im Durchschnitt 80 Bestellungen, mit einer Streuung von 29.”

Damit haben wir nun das normale Verhalten des Systems “Webshop” definiert. Alles, was unter dieser Annahme (Mittelwert 80, Streuung 29) zu unwahrscheinlich ist, interpretieren wir so, dass es kein “normaler Tag” war – irgendetwas ist passiert. (Später werden wir noch sehen, dass im vierten Quartal des Jahres 2010 ziemlich viele Tage unnormal sind.)

Einmalige Ereignisse erkennen

Die Linien ober- und unterhalb des Mittelwertes (X) teilen die Bestellzahlen in Bereiche ein: Die meisten Werte befinden sich innerhalb der Bandbreite von “einer Standardabweichung”, hier: 80 ± 29,0, also zwischen 51 und 109 (gepunktete Linie). Zwischen 2σ und 3σ finden wir nur noch wenige Werte. Jenseits der 3σ-Linie beginnt dann der Bereich der “Ausreißer”, das heißt, “normalerweise” kommt so etwas nur ganz selten zufällig zu Stande. Daher sollte man immer nach einer Ursache forschen, wenn man Werte jenseits von 3σ sieht. In unserem Beispiel beginnt dieser Bereich bei 167 Bestellungen. (Drei Standardabweichungen nach unten würden negative Bestellzahlen bedeuten, daher habe ich das nicht dargestellt.)

Warum gerade 3σ und nicht 4σ oder 2,5σ? Weil sich 3σ in vielen praktischen Anwendungen bewährt hat, denn “falscher Alarm” kommt nicht allzu oft vor. So liegen z.B. bei normalverteilten Größen nur 0.3% der Werte außerhalb des 3σ-Bereiches, d.h. wir würden nur einmal im Jahr einen falschen Alarm sehen, wenn wir täglich einen Wert eintragen.

---

Was ich hier beschreibe wurde im Rahmen der “Statistischen Prozesslenkung” (statistiscal process control - SPC) entwickelt, einer Vorgehensweise zur Optimierung von Produktionsprozessen. Dort interessiert man sich z.B. dafür, welche Schwankungen in den Abmessungen eines Werkstücks zufällig sind, und ab wann man sich fragen muss, inwiefern etwas mit der Maschine nicht stimmt, auf der sie gefertig wurden.

In unserem Beispiel sind es die täglichen Bestellungen eines britischen Webshops, es gibt aber noch viele andere potenzielle Anwendungen in der IT:

• Metriken des Software-Lieferprozesses, wie neu entdeckte Bugs pro Woche, Releases pro Zeiteinheit usw.
• Betriebs-Metriken wie “Mean time to recovery”, “Change fail rate”
• Performance-Metriken, etwa Antwortzeiten

---

Zurück zum Webshop-Beispiel… Man teilt die Werte in drei Bereiche ein:

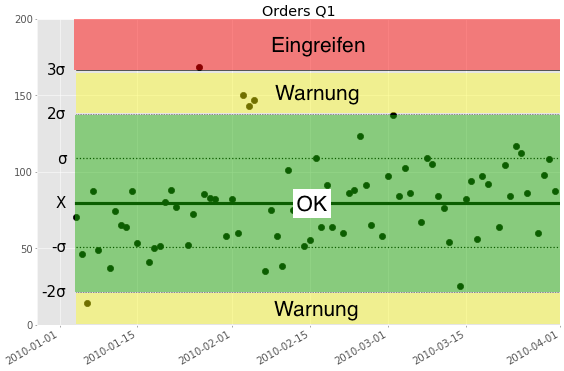
1. Innerhalb von ±2 Standardabweichungen um den Mittelwert herum ist der Normalbereich. (“grüner Bereich”)
2. Werte, die nicht im Normalbereich liegen, aber noch weniger als ±3 Standardabweichungen vom Mittelwert entfernt sind, gehören zum Warnbreich. (Hier gelb dargestellt)
3. Zum Eingriffsbereich gehören alle Werte, die mehr als 3 Standardabweichungen über oder unter dem Mittelwert liegen. (Hier rot dargestellt)

Das Wort Eingriffsbereich (Control Zone) passt besser zur Qualitätskontrolle (für die die Statistische Prozesslenkung erfunden wurde). Dort ist es egal, ob ein Werkstück zu lang oder zu kurz geraten ist, beides ist ein Mangel. In unserem Zusammenhang, E-commerce, würden wir nicht direkt “eingreifen”, wenn es mal mehr als 167 Bestellungen sind, aber wir würden schon wissen wollen, ob es eine Ursache dafür gibt. In unseren Daten gibt as am 26.1. stattliche 168 Bestellungen, das liegt gerade auf der Grenze des oberen Eingriffsbereichs. Vielleicht hat ja eine Marketingkampagne gut funktioniert? Oder eines unserer Produkte wurde in den Nachrichten erwähnt? Vielleicht mussten auch nur liegengebliebene Bestellungen vom Vortag abgearbeitet werden?

Per Zufall würde ein Wert im Warnbereich (gelb) mit einer Wahrscheinlichkeit von 1:40 landen, wenn man normalverteilte Werte voraussetzt. Das würde bedeuten, dass wir an ca. jedem 40. Tag eine “Warnung” bekommen würden, die nur der zufälligen Schwankung der Bestellungen geschuldet wäre. Daher verlangt man, dass mindestens zwei Werte hintereinander im Warnbereich sind, bevor man es als “Signal” für eine nichtzufällige Schwankung auffasst.

Wir haben damit schon zwei Regeln für “Signale”, d.h. Situationen, in denen unser Manager sich auf Ursachenforschung begeben sollte:

• Signal 1: Wenn ein Wert im Eingriffsbereich (rot, jenseits von +3σ oder -3σ) landet
• Signal 2: Wenn mindestens zwei aufeinanderfolgende Werte im Warnbereich (gelb) landen

In unseren Daten sehen wir vom 3.-5. Februar eine Gruppe von drei Werten, die im Warnbereich zwischen 138 und 167 liegen. Dies sind ja reale Daten aus einem Webshop in Großbritannien, ich konnte leider keine mögliche Ursache finden. In diesem Shop gibt es Geschenkartikel, es scheint aber Anfang Februar keinen besonderen Anlass für Geschenke in UK zu geben.

Das folgende Diagramm zeigt den Verlauf der Bestellungen über das gesamte Jahr, wobei ich die Signale aus dem roten und gelben Bereich hervorgehoben habe:

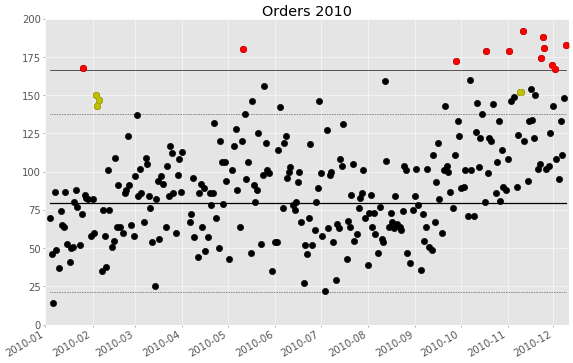
Wir sehen im Mai noch einen Tag mit sehr vielen Bestellungen (roter Punkt), und im Jahresendgeschäft häufen sich die guten Tage. Es gibt nur zwei Zeitabschnitte mit gelb hervorgehobenen Punkten: wie erwähnt vom 3. bis 5. Februar, und dann noch zwei Tage im November.

Systematische Veränderungen erkennen

Die obigen Regeln geben uns Signale für “besondere Tage”, d.h. im allgemeinen Einmaleffekte wie eine gelungene Marketingaktion oder den Ausfall des Webshops. Daneben sind aber auch allmähliche Änderungen im “System Webshop” denkbar, die zu einem systematischen Anstieg (oder Abfall) der Bestellungen führen. Könnte ja sein, dass wir immer besser darin werden, den Webshop zu betreiben, oder dass im Laufe der Zeit unsere Antwortzeiten immer länger werden, worunter dann die Umwandlungsquote (conversion rate) leidet.

Für das Erkennen von Trends gibt es noch zwei weitere Signale:

• Signal 3: Wenn 8 oder mehr Werte hintereinander ansteigen (bzw. wenn 8 Werte fallen)
• Signal 4: Wenn 7 oder mehr Werte hintereinander oberhalb der Mittellinie X sind (bzw. alle Werte unterhalb der Mittellinie)

Das lässt sich wieder mit Wahrscheinlichkeiten begründen: Wenn die Schwankungen rein zufällig sind, dann geht es mit gleicher Wahrscheinlichkeit auf- wie abwärts. Siebenmal hintereinander aufwärts ist entsprechend unwahrscheinlich (0,5^7 = 1:128, weniger als 1%). Bei zufälligen Schwankungen erwarten wir auch, dass die Werte mit gleicher Wahrscheinlichkeit ober- wie unterhalb der Mittellinie landen. Siebenmal hintereinander unterhalb (bzw. oberhalb) der Mittellinie ist wieder unwahrscheinlich.

Wenn wir diese Auswertung für die Webshopdaten machen, bekommen wir dieses Bild:

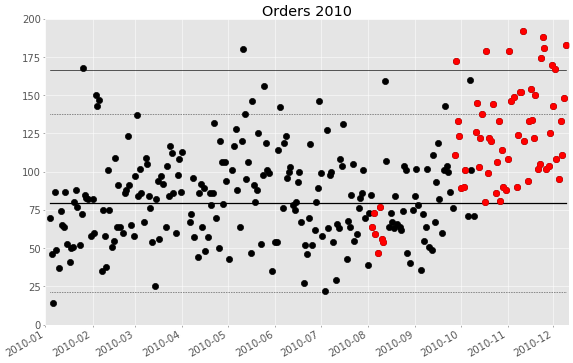
Es gab keinen einzigen Trend zu Signal 3 (mit acht oder mehr Werten die konsistent steigen oder fallen). Dafür sehen wir zwei Zeiträume, in denen auffällig viele Werte ober- bzw. unterhalb der Mittellinie liegen (Signal 4):

• Die erste Augustwoche sieht schwach aus. Das ist vielleicht der Ferienzeit geschuldet.
• Im vierten Quartal sind fast alle Tage über der Mittellinie, das ist sicher das Jahresendgeschäft. Das entsprechende Signal würden wir am 3. Oktober bekommen.

Im vierten Quartal gibt es also eine systematische Änderung, die wir erkennen und der Ursache “Jahresendgeschäft” zuordnen könnten. Nun kann es ja auch im Weihnachtsgeschäft Probleme mit dem Webshop und entsprechend “schlechte Tage” geben. Daher sollte man für diesen Zeitraum einen neuen Vergleichszeitraum definieren, z.B. das letzte Quartal des Vorjahres.

Auch wenn Ihr Geschäft stetig wächst, werden Sie gelegentlich einen neuen Vergleichszeitraum wählen, oder ein zu erwartendes Wachstum in die Mittellinie einarbeiten.

Schwankungen richtig einordnen

Der Manager aus unserem Szenario würde also nur an wenigen Zeitpunkten tätig werden müssen:

• Am 26. Januar, ein außergewöhnlich guter Tag mit 168 Bestellungen (Signal 1)
• Am 3.-5. Februar, drei gute Tage mit 150, 143, 147 Bestellungen (Signal 2)

Da diese Zeitpunkte noch in den Vergleichszeitraum (1. Quartal) fallen, würde er die Signale leider erst am 1. April bemerken, aber immerhin…

• Am 11. Mai, noch ein außergewöhnlich guter Tag mit 180 Bestellungen (Signal 1)
• In der ersten Augustwoche, wo mehrere Tage hintereinander weniger als 80 Bestellungen ankommen (Signal 4)
• Ab 28. September, wo ein guter Tag mit 172 Bestellungen den Startschuss für das Jahresendgeschäft gibt. (Signale 1 und 4)

An allen anderen Tagen kann er sich darauf konzentrieren, das System “Webshop” grundsätzlich zu verbessern, so dass die Zahl der Bestellungen systematisch wächst, statt nur zufällig um die Mittellinie zu streuen. Etwa Antwortzeiten verkürzen, besseren Traffic generieren, oder den Checkout-Prozess vereinfachen.

Was ich hier anhand eines öffentlich zugänglichen Ecommerce-Datensatzes vorgeführt habe, beruht auf einfachen und robusten Verfahren, die sich jahrzehntelang zumindest in der Fertigung bewährt haben. Neben den hier vorgestellten Signalen 1 bis 4 gibt es noch weitere Regeln und Abwandlungen, die Grundideen bleiben aber dieselben:

1. Ein einzelner Wert lässt sich nicht interpretieren. Metriken muss man in ihrem historischen Kontext betrachten.
2. Ermitteln Sie den zu erwartenden Mittelwert und die Schwankungsbreite der Metrik aus historischen Daten.
3. Die beste Metrik nützt nichts, wenn sie nicht zu sinnvollen Handlungen führt. Daher sollten Sie nicht zufälligen Schwankungen hinterherjagen, sondern auf der Grundlage von vorher festgelegten Entscheidungsregeln (Signale 1-4 o.ä.) reagieren.

Wenn Sie tiefer einsteigen wollen, kann ich Ihnen das Fachbuch “Statistical Process Control” von John S. Oakland empfehlen.

Und falls Sie noch nicht wissen, ob es in Ihrem Kontext relevant sein könnte: Mark Graban beweist in seinem Buch “Measures of Success” dass dieses Thema überhaupt nicht trocken und schon gar nicht auf die Fertigung beschränkt sein muss.

Matthias Berth