Ein wichtiger Baustein für quantitative Geschäftsmodelle ist der Customer Lifetime Value (CLV):

Wieviel Gewinn bringt ein Neukunde über seine gesamte “Lebenszeit”?

In stabilen Geschäftsmodellen bildet der Customer Lifetime Value eine theoretische Obergrenze für alle kundenbezogenen Ausgaben. Die Gewinnung eines Neukunden sollte beispielsweise auf keinen Fall teurer sein als sein CLV. Bei SaaS (Software as a Service) gibt es die Faustregel: Die Akquisekosten sollten 1/3 des CLV nicht überschreiten.

Oft reichen Durchschnittswerte aus, aber man kann das natürlich beliebig verfeinern:

• nach demografischen Faktoren (Machen Frauen mehr Umsatz als Männer? Junge Leute mehr als alte?)
• nach Marktingkanal (Kundinnen, die über Empfehlungen gekommen sind, wandern weniger häufig ab?)
• nach Kundenbindungsprogramm (Mitglieder von Amazon Prime machen sicher mehr Umsatz.)

Ich will die Diskussion hier weiter vereinfachen und die Kostenseite ganz außer acht lassen, wir reden also nur über den Umsatz über die gesamte “Lebenszeit” eines Kunden.

Das einfache Modell für Kundenbindung lässt sich manchmal auch hier anwenden: Alle Kunden-Kohorten schmelzen monatlich mit einen festen Prozentsatz (der Abwanderungsrate) ab. Wir legen einen festen Warenkorbwert zugrunde, also ist Umsatz proportional zur Kundenzahl. Im Mai 2019 haben wir mit der Kohorte von Neukunden noch 100% Umsatz gemacht, einen Monat später verlieren wir vielleicht 40% der Kunden, haben also auch nur noch 60% des Umsatzes, und so weiter.

Es gilt genau dieselbe Argumentation wie beim Abwanderungsverhalten:

Gesamtumsatz = Warenkorbwert * (1 / Abwanderungsrate)

In unserem Beispiel war die Abwanderungsrate 40%, also ist der Gesamtumsatz (Customer Lifetime Value) gleich 2,5 * Warenkorbwert. Für jeden Euro an Umsatz mit Neukunden diesen Monat können wir entsprechend noch weitere 1,50€ Umsatz in der Zukunft erwarten. Im Observable Notebook ist so eine Beispielrechnung schon enthalten. (Man müsste zukünftige Umsätze noch abzinsen, um Zahlungsströme über verschiedene Zeiträume vergleichbar zu machen)

Was kann man tun, wenn die Kohorten nicht nach unserer einfachen Regel mit einer festen Abwanderungsrate von x% pro Monat abschmelzen? Dann muss man eben die tatsächlich beobachteten Abwanderungsraten verwenden:

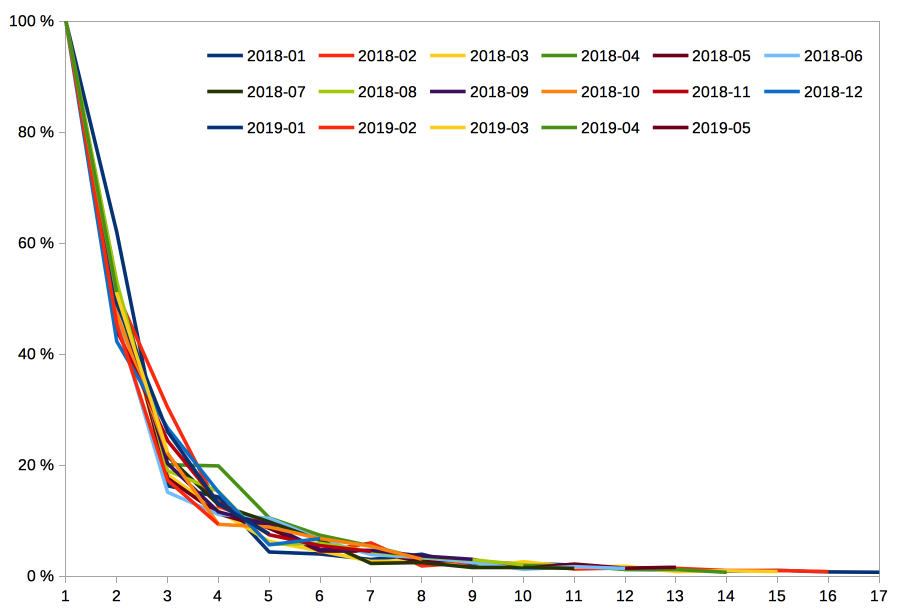
Eine Linie in diesem Diagramm ist eine Kohorte, die x-Achse ist das Alter der Kohorte in Monaten, die y-Achse ist der im jeweiligen Monat gemachte Umsatz (Das hier sind simulierte Daten, die einer realen Situation ziemlich nahe kommen). Um die Kohorten vergleichbar zu machen, setzen wir den ersten Monatsumsatz zu 100%. Jetzt bilden wir das Mittel (oder den Median) über die Kohorten eines Alters: voilà, das sind die empirisch beobachteten Kundenbindungsraten.

Für die oben dargestellten Kohorten sehen die durchschnittlichen Monatsumsätze so aus:

Alter	Monatsumsatz
 1	100,00 %
 2	 49,63 %
 3	 23,19 %
 4	 13,26 %
 5	  8,33 %
 6	  5,43 %
 7	  3,72 %
 8	  3,02 %
 9	  2,33 %
10	  1,89 %
11	  1,71 %
12	  1,46 %
13	  1,36 %
14	  0,93 %
15	  0,88 %
16	  0,82 %
17	  0,85 %

Lesehilfe: Im Monat 12 machen wir durchschnittlich nur noch 1,46% des Neukundenumsatzes mit einer Kohorte.

Der Customer Lifetime Value ist kein exakter Wert, vielmehr machen wir eine Vorhersage aufgrund vorhandener Daten und Annahmen. Für die Neukunden, die wir in diesem Monat gewinnen, nehmen wir an, dass der Umsatz nach der obigen Tabelle abschmelzen wird. Wir sollten die Vorhersage nicht allzu weit in die Zukunft ausdehnen, schließlich kann sich unser Angebot und auch das Marktmmfeld schnell ändern. Im vorliegenden Beispiel würde ich auf der sicheren Seite bleiben und die Umsätze nach Monat 17 pauschal mit 0% ansetzen.

Der Customer Lifetime Value beträgt dann 218,8% des Neukundenumsatzes (= Summe der zweiten Spalte). Anders ausgedrückt: Für jeden Euro Neukunden-Umsatz können wir noch weitere 1,19€ Umsatz in der Zukunft erwarten.

Dies können wir nun für die Entscheidung für oder gegen ein neues Feature (oder eine Marketingmaßnahme) nutzen. Ein Beispiel: Wenn Feature X uns voraussichtlich 100.000 neue Besucher auf die Website bringt, werden daraus 3000 Neukunden (Umwandlungsquote 3%), mit einem Warenkorbwert von 50€, mithin einem Umsatzpotenzial von

3000 * 50 € * 2,188 = 328.200 €

Wenn wir dann noch unsere Umsatzrendite von 20% ansetzen, bekommt die ganze Maßnahme einen voraussichtlichen Wert von 20% * 328.200 € = 65640 €.

Matthias Berth